Torufyymの日記

2024/1/1: 問題のある表現を一部修正、偏微分についての注意と例題を一つ追加

0. アブスト ラクト

　実三次元直交座標系におけるベクトル解析の公式を、完全反対称テンソルε等とアインシュタインの縮約記法を使った内積・外積の表現を使うことで（答えに形を合わせていくことなく）自然に導出できることを紹介します。

　円筒座標系・球（三次元極）座標系・四次元以上の座標系における公式については著者の乏しい数学力のため議論していません。

1. イントロダクション

完全反対称テンソルを使ってぱぱっとかっこよく導出する術を身につけて、「ベクトル解析　公式」で検索するのをやめましょう。

2. 前提知識

記法

アインシュタインの縮約記法を少し変えたものを用います。

総和記号は省略しますが、2つのiが同じ項に出現しているときはiについて和をとっています(普通は上付きと下付きが一つずつの場合に和をとると書きますが、後述する理由により、そうはしません）。この記事では添字は全て1, 2, 3を走ります。

完全反対称テンソルの基本的性質

この記事で使う完全反対称テンソルは、 $\varepsilon^{123} =1$ を満たします。

初めてこのεを見るという方は脚注→*1 *2を見てください。

次の公式は重要なので言及しておきます：

3. 準備

実ベクトルの内積は一般的に次のように書けましたね。（本来の定義）

ただしgは計量テンソルです。また、ベクトルAの第n成分を $A_n$ と書いています。今から議論する三次元直交座標系では $g=$ diag $(1,1,1)$ と、単位行列なので、これからの導出においては上付き添字と下付き添字を区別する必要はありません（しません）。興味は素早く導出することにあるので、大胆に計量を省略しちゃおうと思います。なのでアインシュタインの縮約記法とは少し違って「二つ同じ文字があればその文字で和をとる」という言い方をしました。気持ち悪い人は適宜 $g^{ij}$ を補いながら読んでください。

この記事での内積は次のように書きます。（この記事での定義）

次に、外積は次のように書けます。

ここでも添字が気持ち悪い*3ですが、我慢してください。

重要なのは添字の対応です。この記事で一番重要なのでまとめます。

微分演算子∇は次のようにしておきます。スカラー値関数（ベクトル値関数の成分もこれとみなせるとします）f, gについて積の微分公式があるとしておきます。

3. 早速やってみよう

①A×B=-B×A :外積の反対称性

外積の添字のルールを確認しながら、証明（？）を見てみましょう。

任意の成分iについて示せたのでOKということです。符号反転は $A_j B_k$ の入れ替えではなく反対称テンソルの添字入れ替えによるものだというのがポイントです。

②A・(B×C) = B・(C×A) :スカラー三重積

丁寧に私たちの言葉に翻訳していけば大丈夫です。翻訳の過程をあえてあらわに書いてみます。

ここまでこれたらこっちのものです。 $\varepsilon$ もスカラーなので入れ替えてよくて、

最後の変形を見てください。二つのベクトルの成分が共にj成分だったので、内積として書き換えることができました。だんだん添字の感覚が掴めてきましたか？

③A×(B×C) = (A・C)B-(A・B)C :ベクトル三重積

ちょっと気持ち悪い公式ですよね。どのように示されるでしょうか。まずは私たちの言葉に書き換えましょう。

今一度外積の書き換えルールと見比べるとよりよく理解できると思います。さて、こんな時に使える公式を用意していたので、書き換えましょう。（再掲）

「この公式を覚えるのが嫌だ」あるいは「なんで成立するのか直感的にわからんぞ」という人はこの脚注→*4 *5をご覧ください。εの性質を少し考えると、次から覚えなくても使えると思います。

ここまで来ればもう形が見えたのではないでしょうか！

読むのをやめないで

全然自然に導けていないじゃないか！結局公式に頼りおって！！！と怒り出す人、ごめんなさい。しかし、注目してほしいのは、一貫して「添字を減らしていく」という方針で結論まで至っていて、よくある「結論の形に合わせにいく」ような変形が一切ないという点です。結論の形がわからなくても、ひたすら添字を減らしていけば導出できるのです。嬉しい。

説明が多くなったので、今の証明をダイジェストで振り返りましょう。実際に私がパッと導出するときの行間はこんな感じだと思います。

4. 本領発揮：微分公式篇

この章の内容に入るために少しだけ説明を書いておきます。ただ、「今読んでも別に大したことだと感じないけど後で役に立つかもしれない」タイプの注意点なので、軽く流して④以降を見て、困ったら戻ってきていただければと思います。

・ $\partial_i f$ はfの $x^i$ による偏微分。どこまでを偏微分するかが（積の微分の話になるので）重要です。基本的に関数2つ以上の積に $\partial$ がかかっている場合は()で範囲を明示します。()がない場合は次の関数(定数は除く)にかかっています。

・各 $f, A_i$ 等は関数です。今独立変数として $x^1 ,x^2 ,x^3$ がありますが、 $A_i = A_i (x^1 ,x^2 ,x^3)$ というようにこの全てに依存しているものとして計算していきます。なので例えば $\partial_1 A_2$ と添字が違っていても0にはなりません。また、順序交換も一般には不可能で、 $A_i \partial_i A_j = \partial_i (A_i A_j) - A_j \partial_i A_i$ といった関係を使うことになります。

・一方、 $\varepsilon^{ijk}$ は（i, j, kに依存していますが） $x^1 ,x^2 ,x^3$ のいずれにも依存していないという意味で定数です。したがって、偏微分作用素に関し $\partial_l (\varepsilon^{ijk} f) = \varepsilon^{ijk} \partial_l f$ のように順序交換が可能です。ただし、 $\partial_i$ が作用する相手がいなくなるような場合は不可とします(e.g. $\partial_l \varepsilon^{ijk} = \varepsilon^{ijk} \partial_l$ は不可)
(2024/1/1追記)

④∇・(fA) = ∇f・A+f∇・A (i.e. div fA = grad f・A+f・div A)

特に大きく変わることはないです。積の偏微分ですね。

⑤∇・(A×B)=B・(∇×A) - A・(∇×B)

スカラー三重積とは形が違うんですよね、しかも謎のマイナスが...これは反対称テンソルの方法だと自然に出てきます！

途中、εはスカラー定数だから∂と入れ替えても問題ないことに注意しましょう。このように、「積の微分はそれぞれに分けよう」という当たり前の発想で、あとは外積の形を作るだけで完結しました。楽しくなってきましたよ。

(2024/1/1　公開時点でεはスカラーだから、と書きましたが、言い方が間違っていました。εが $x^1 ,x^2 ,x^3$ の関数ではないことが本質なので、「定数」に修正しました。)

⑥∇×(fA)=∇f×A+f∇×A

(´-ω-)ｳﾑｳﾑ

⑦∇×∇f = 0 (i.e. rot grad f=0)

E=-∇φ-∂_t Aというようにスカラーポテンシャルを導入するときのやつですね。公式のイメージ的にはそりゃそうだろ感があるんですが、真面目に展開してやろうとすると面倒臭い、という公式です...

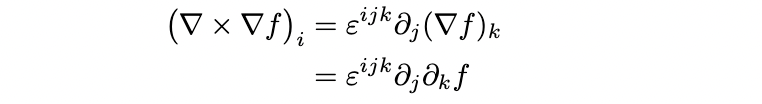
ここで詰まっちゃうかもしれませんが、この二つの∂は入れ替えても同じです*6！だから、この項はj, kについて反対称テンソル×対称テンソルなので直ちに0とわかります。一応例を出すと、i=1の場合、

と、消えてくれますね。

⑧∇・(∇×A) = 0 (i.e. div rot A = 0)

こちらはB=∇×Aとベクトルポテンシャルを導入する際の根拠となる*7公式ですね。こちらもさっきと同じノリです。

注意深い読者は、さっきみたいにj, kを動かそうとすると $A_k$ も変化してしまうじゃないかと思うかもしれません。しかし、さっきやったのは本質的には「偏微分作用素の入れ替え」で、それなら今の場合動かすべき添字はi, jです。kを固定してi, jを動かせば、 $A_k$ を固定したまま、ちゃんと消えてくれますよ。

⑨∇×(∇×A)=∇(∇・A)-∇²A

9面のラスボスです。この記事はこの問題で終わりです。勘の良い読者はこの展開式を見て「さっきの二つεがあるときの公式を使いそうだな」と思ったかも。大正解です。

わかんなくなった人は、③に戻ってください。詳しめに説明してあります。

小まとめ

このやり方で、色々な公式を割とすっきりと自然に導出できます。見てるだけだと面倒に見えるかもしれませんが、私がかなり行間を小さく書いているからというだけで、手を動かしてみれば「めっっちゃ簡単じゃん！」と思えると思います。

以上、長い記事を読んでくれてありがとうございました。お疲れ様でした。良いお年を。　冬山徹

⑩A×(∇×A)=(1/2)∇(A・A) - (A・∇)A

あけましておめでとうございます。嬉しいことに1/1の午前8時という時間にTwitterで質問を頂いたので共有します。人とたくさん数学・物理の議論ができる一年になるといいなと思っていたところだったので、幸先が良いです。

さて、例によって私たちの記法に書き換えましょう。一つ上の⑨と同様に、

とできます。最後のA・∇はもちろん $A_1 \partial_1 +A_2 \partial_2 +A_3 \partial_3$ のことです。あとは第一項をうまく内積の形にしたいです。添字を減らすという方針の一環と捉えればこれも自然な変形ですね。

であるので（ $\partial (fg) = f\partial g + g\partial f$ を思い出してください)、これを使って、さらに $A_j A_j$ は内積でかけて、まとめて

を得ます。

5. まとめ

いかがでしたか？この記事では、最近話題になっている、完全反対称テンソルを用いたベクトル解析の公式の導出方法について、調査してみました。

残念ながら、何がなんだかよくわかりませんでしたが、わからなくなるとつい「ベクトル解析　公式」でググってしまいますよね。

調べてみると、ベクトル解析の公式の良い導出方法が見つかるかもしれません。やはり数学は奥が深いですね。それでは、次の記事でお会いしましょう！

*1:εの肩に添字が3つありますが、これは累乗ではありません。3つの変数値i, j, kを受け取って値を返す関数(写像)とみなせるものです(ijkとありますが、積ではないです)。今回の記事での定義域値域を書くとε: {1, 2, 3}³→{-1, 0, 1}という感じでしょうか。i=1, 2, 3, j=1, 2, 3, k=1, 2, 3の場合だけ考えればokです。

*2:具体的な性質はこうです。i, j, kに同じ数字が2回以上現れる場合(112, 111, 323など)はεは0です。全て相異なる場合は、i, j, kが偶置換(1, 2, 3, 1, 2, ...の順番)ならεは1, 奇置換(3, 2, 1, 3, 2, ....の順番)ならεは-1です。言い換えれば、(i, j, k)=(1, 2, 3)の状態ではεは1なんですが、ここから一つのペアを入れ替える(i↔︎j, j↔︎k, i↔︎k)たびに符号が反転します。具体例：132→-1, 312→1, 321→-1, ...

*3:εの添字も含め下付きに統一すればまだいいんですが、それは流石になんか許せない気持ち悪さでした。。。

*4:まず、i,j,kは相異なるとし、k,l,mは相異なるとします。なぜなら、同じ数字があると0になり、全体も0となるからです。こうすると、i, j, kとk,l,mがそれぞれ1, 2, 3の並び替えになります。今k=1とすると、kはどちらにも含まれているので、i,j とl, mがそれぞれ2, 3の並び替えとなります。よって、「i=l かつj=m」か「i=mかつj=l」の二通りです。他のkでやってみても、同じ結論になります。この二つだけ考えれば良いので、出てくる項は2つで、しかもδ関数2つの積で、和をとった時文字が2つ消えるようになっているわけです。この2パターンの内、i,j,kとk,l,mの置換性を調べると、前者では(i, j, k), (k, i, j)となって偶にせよ奇にせよ同じ置換性で後者では逆（偶置換と奇置換1つずつ)となるので、εの積の部分はそれぞれ1, -1と確定します。

*5:改めて要約すると、(i)kが共通なので、全体がゼロにならないのは(i, j)と(l,m)が同じか逆の時だけ(ii)前者は二つのεの置換性が同じで、後者は逆なので符号は1, -1　ということです。わ、分かりましたか...? 説明下手でごめんなさい...

*6:いつもそうではないけど、ベクトル解析では二階の偏導関数が非可換な性質の悪いfは出てこないと思います...。というか普通に証明する場合でもこれは仮定することになるので、許してください！

*7:ヘルムホルツ分解（任意のベクトル場Bに対してスカラー場fとベクトル場Aが存在してB=∇f+∇×Aが成立する）から説明を始めるべきですよね。Aがあったら確かにB=∇×Aで∇・B=0になるけど、他の要件も満たしているAがあるかは非自明なのに、いっつも誤魔化されてきたところです。私も誤魔化します✌️